
분산분석(analysis of variance)
회귀모형의 설명력과 유용성을 분석하는 효과적인 방법을 보통 ANOVA라고 합니다
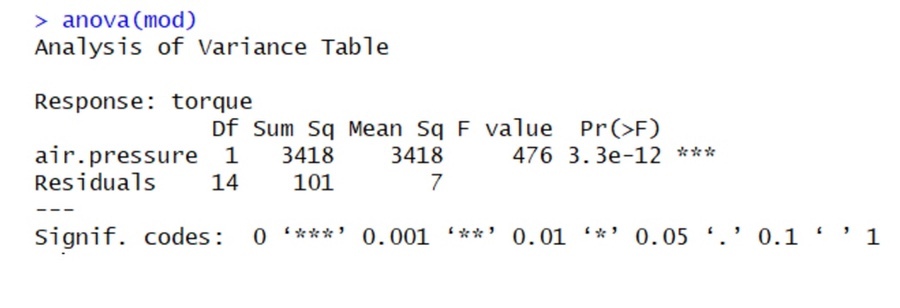
제곱의 합의 계산
* SST (total variation of response)
yt의 y 평균 주변에서의 총 변동을 측정
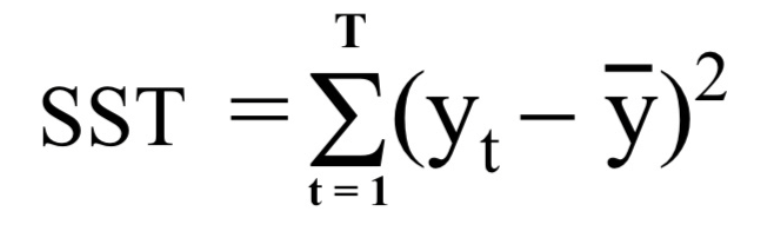
* SSR (regression sum of square)
- the variation explained by the linear relationship
추정회귀식의 y값과 y평균값의 차를 모두 더한 값
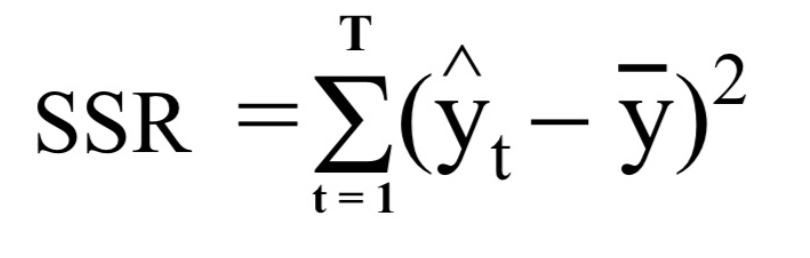
* SSE (error sum of square)
unexpected variation among total variation
추정회귀식과 원래 y 값의 차를 모두 더한 값
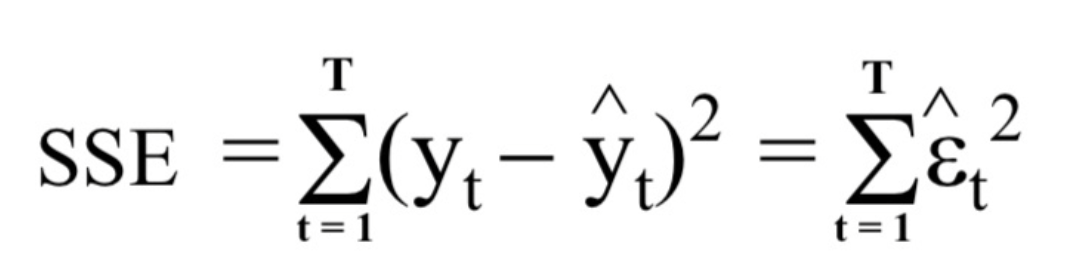
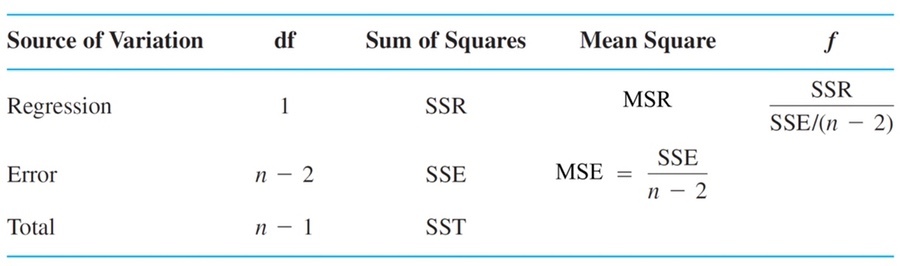
결국 SSR, SSE, SST 모두 차이의
제곱의 합으로 분산을 나타낸다고 할 수 있어요
그래프로 나타내면 아래와 같이 표현할 수있어요 ☺️
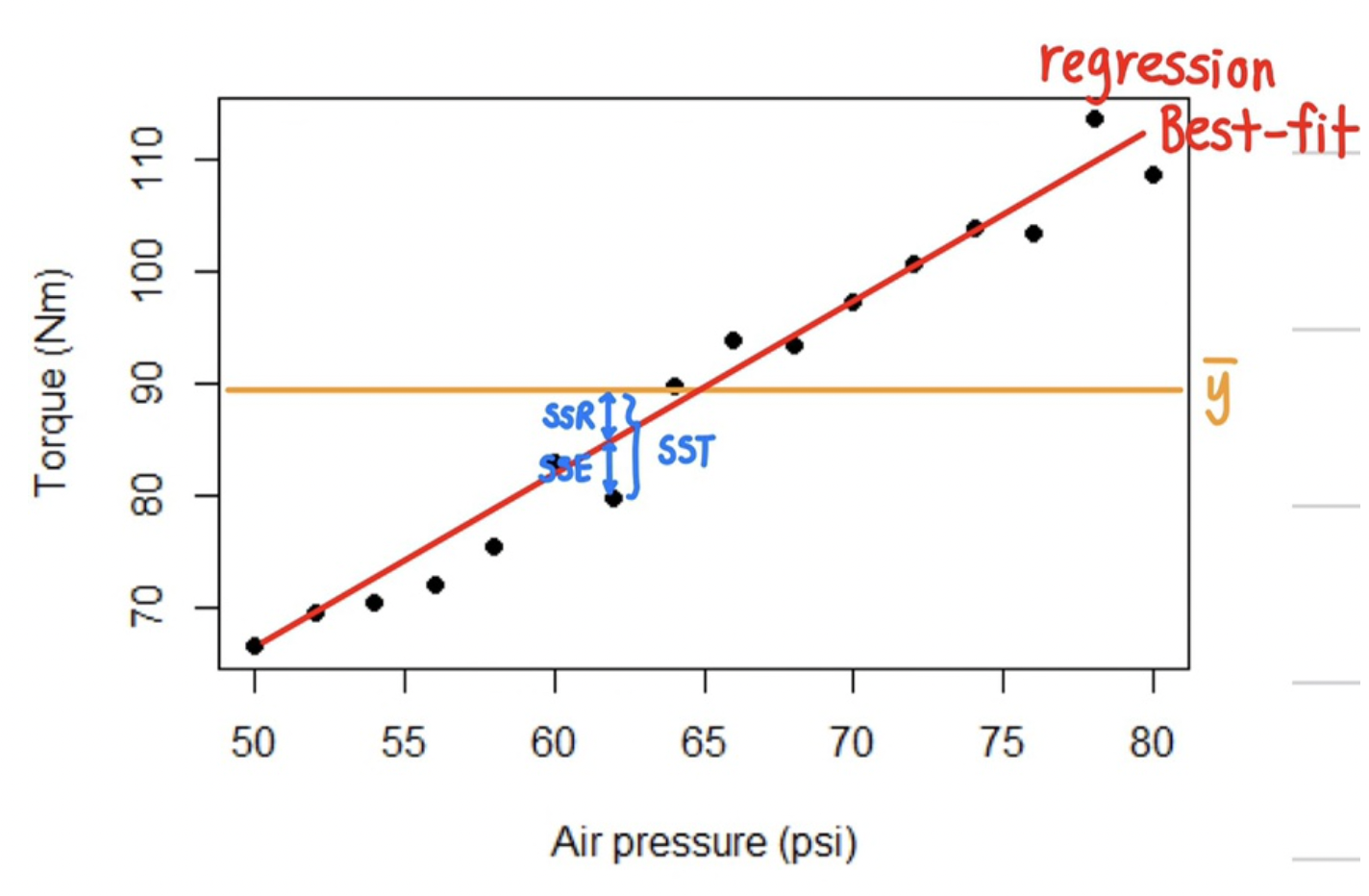
df (degree of freedom) 자유도
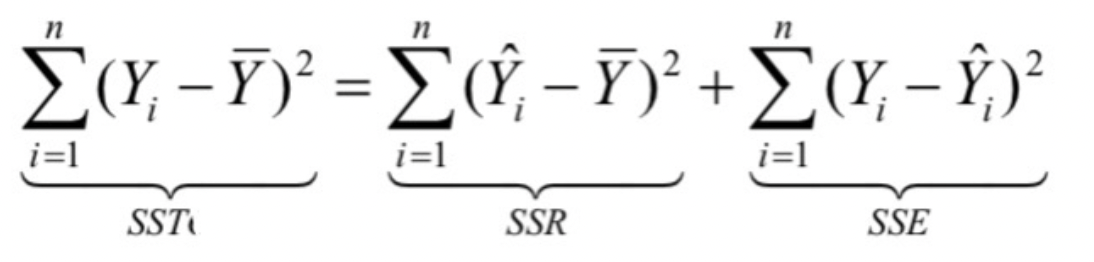
자유도도 마찬가지로 SST = SSR + SSE가 성립되죠
• df_ SST = n-1
• df_SSR = 1
• df_SSE = n-2
모델 유의성 평가 방법 model significance method
회귀 분석결과 독립변수가 종속변수를 얼마나 잘 설명하고 있는지 측정을 위해 유의성평가를 하게됩니다
1) coefficient of determination 결정계수

결정계수는 0에서 1사이의 값이며 1에 가까울수록 모델의 오차 추정값이 적어져서
모델이 유의하다고 결론지을 수 있어요
2) Test statistic (f 분포)
위에서 설명한 것과 같이 SSR과 SSE은 일종의 분산을 나타낸다고 할 수 있기때문에
둘다 카이제곱분포를 따르는 것을 알 수 있어요
* 카이제곱분포란, 각각 독립인 표준정규분포를 따르는 확률분포의 제곱의 합 X가 따르는 확률분포 입니다
카이제곱분포를 따르는 두 변수를 나누면
F분포를 따르게 되어 우리는 SSR/SSE가
얼마나 큰지는 해당되는 F분포를 찾아서 확인할 수 있어요

만약 x와 y의 선형관계가 없다면 SSR의 값이 작아지게되어 f (test stastic 검정통계량) 값이 작아지게되겠죠

critical value보다 f 검정통계량이 크다면 귀무가설을 reject하므로 모델은 유의미하다고 결론지을 수 있어요

#분산분석 #검정통계량 #f분포 #데이터분석 #SSR #SSE #결정계수
'Data Science > statistics' 카테고리의 다른 글
| [데이터 분석] 일원분산분석 Tukey's procedure (0) | 2022.04.21 |
|---|---|
| [데이터 분석] 일원분산 분석_one way ANOVA (0) | 2022.04.21 |
| [데이터분석] 다중회귀분석Multiple linear regression (0) | 2022.04.21 |
| [데이터분석] 단순회귀분석 simple linear regression (0) | 2022.04.04 |
| [데이터분석] 통계 기초 정리_확률변수,모집단,표본,가설검정 (0) | 2022.04.01 |