[데이터 분석] 일원분산 분석_one way ANOVA

분산 분석 ANOVA
총 제곱 합(total sum of squares)을 실험과 관련된 요인(인자의 작용)에 대한 각자의 제곱 합으로 분해한 후, 나머지를 오차변동으로 해석하는 검정법
각 요인 마다 분해한 분산을 오차분산과 비교하여 특히 큰 영향을 주는 인자(요인)가 무엇인가를 검정하고 그 결과 유의치가 있으면 요인마다 효과 추정을 행합니다.
따라서 분산분석은 측정치의 변동을 요인 별로 분해하여 어느 요인이 특성치에 어느 정도 영향을 주는지를 파악하는 것이라고 할수있습니다
요인(factor)의 갯수에 따라
일원분산분석(one-way ANOVA,single factor ANOVA),
이원분산분석(two-way ANOVA, two factor ANOVA)로 분류됩니다
오늘은 single factor ANOVA에 대해 자세히 다뤄봅시다
일원분산분석 (single factor ANOVA)
그룹 3개 이상의 평균을 비교하여 서로 유의하게 다른지 판단하기 위해 사용
들어가기 앞서 용어에 대한 정리를 간단하게 하면 좋을 것같아요
· 인자/요인 (factor) 관측값에 영향을 주는 속성 (independent variable)
· 인자/요인 수 (factor level) 인자의 여러 조건
· 처리 (treatment) 인자 수준의 조합
· 반응치 (response) 요인에 반응하는 변수 (dependent variable)
예시를 함께 보면서 요인과 반응을 구분해봅시다
1) A civil engineer is investigating the effects of five different curing methods on the compressive strength of concrete.
curing method 가 요인이 되고 요인의 level갯수는 5개이고,
반응은 compressive strength of concrete가 되는거죠!
2) A wind turbine manufacturer is investigating the effects of three different tower heights on the power generation.
tower height가 요인이고 3개의 다른 요인이 있으며,
반응은 power generation이 됩니다!
일원배치법의 데이터 배열
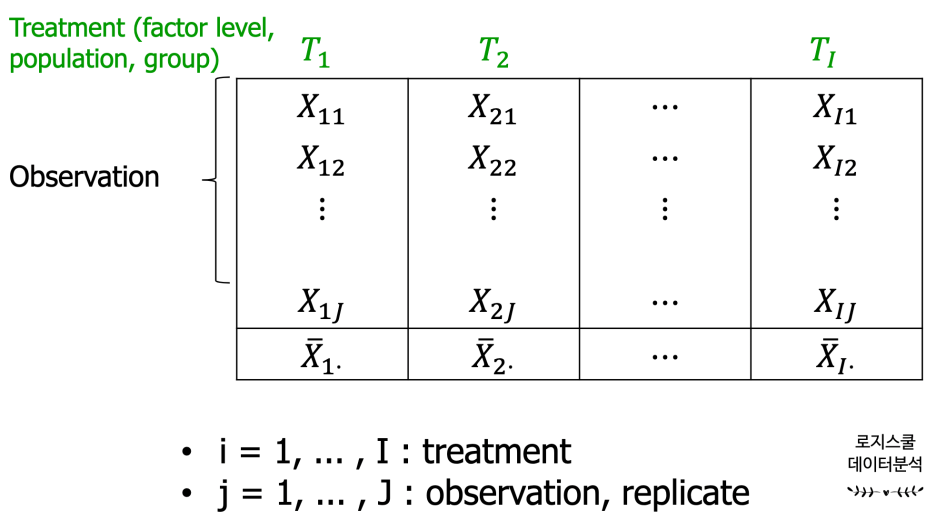
single factor ANOVA의 기본가정
: 각 집단에 해당되는 모집단의 분포가 정규분포이어야 하며, 각 집단에 해당되는 모집단들의 분산이 같습니다
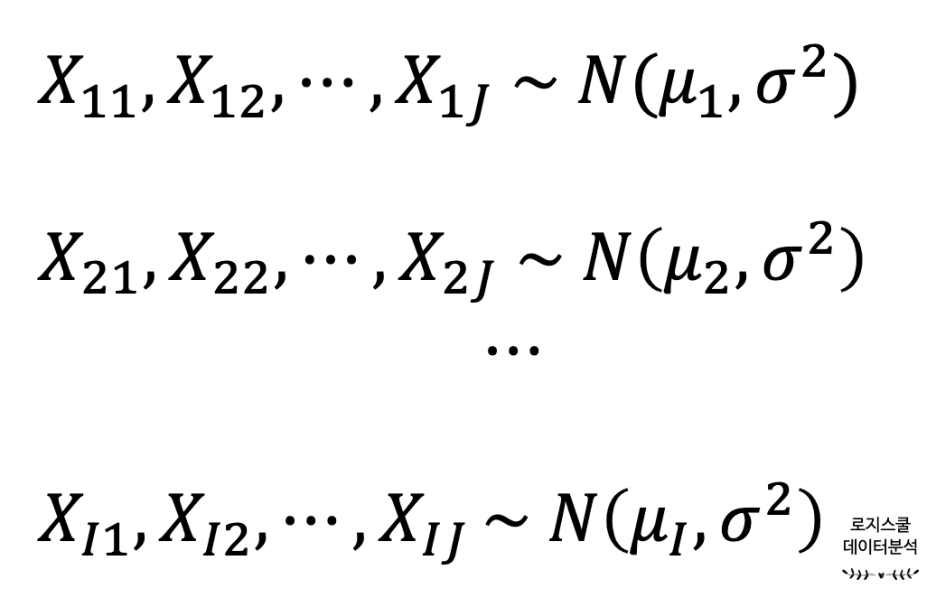

μi : i 집단의 모평균
αi : 인자 A 의 제 i집단의 효과
εij : 오차
그렇다면 위의 각 parameter를 어떻게 추정할까요?

아래의 표에 있는 식을 통해 전체 평균과 각 집단의 평균값을 구할 수 있습니다!

+) 이론적으로 모든 αi 값을 더했을때 0이 나오게 됩니다
